东莞网上做公司网站北京seo关键词排名优化
协方差矩阵与3d高斯
3d高斯与椭球与协方差矩阵
3d高斯,及3维空间内的正态分布。
通过一元正态分布的坐标系图像不难想象,3维空间中的正态分布点集中在一片椭球空间中,各方向长轴取决于各方向正态分布的方差。
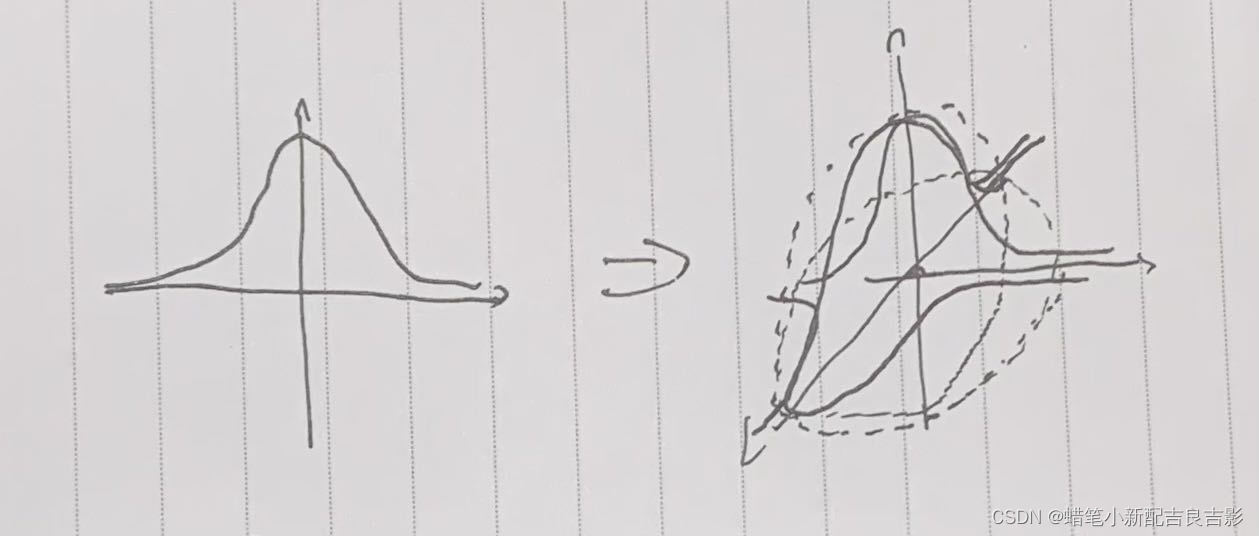
而协方差矩阵通过计算多元之间的协方差关系,反映了椭球在空间中所呈现的几何形态,具体表现方法见下文。
协方差矩阵的几何意义
参考文章:https://www.zhihu.com/tardis/zm/art/37609917?source_id=1005
- 多元正态分布函数表达式如下:
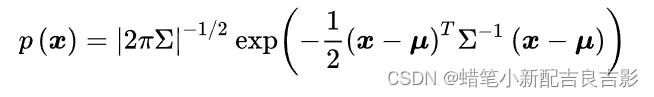
- 可简化为:(忽略常数,μ为0)
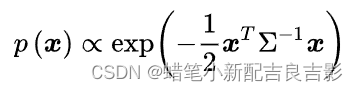
- 考虑线性变换 t = Mx
- 引入缩放矩阵S
3维空间中则在3个轴上进行缩放,需要一个3*3*3的对角线矩阵

- 引入旋转矩阵R

- 通过左乘变换矩阵的规则可知,变化矩阵M = RS
- 又x = M⁻¹t,通过带入化简后的多元正态分布表达式,可以得到
∑ = MMᵀ - 综上可以得到 ∑ = RSSᵀRᵀ
即得到协方差函数所表示的放缩/旋转几何意义
对应该放缩/旋转操作所得到的空间内唯一形状的椭球
及对应唯一的一组3d高斯表达。 - 这样的变换会在后面的加快参数更新中得到应用
